树
在計算機科學中,樹(英語:tree)是一种抽象数据类型(ADT)或是實作這種抽象数据类型的数据结构,用來模擬具有樹狀結構性質的数据集合。
它是由 n(n>0)个有限节点组成一个具有层次关系的集合。把它叫做“树”是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的。它具有以下的特点:
- 每个节点都只有有限个子节点或無子節點;
- 没有父节点的节点称为根节点;
- 每一个非根节点有且只有一个父节点;
- 除了根节点外,每个子节点可以分为多个不相交的子树;
- 樹裡面沒有環路(cycle)
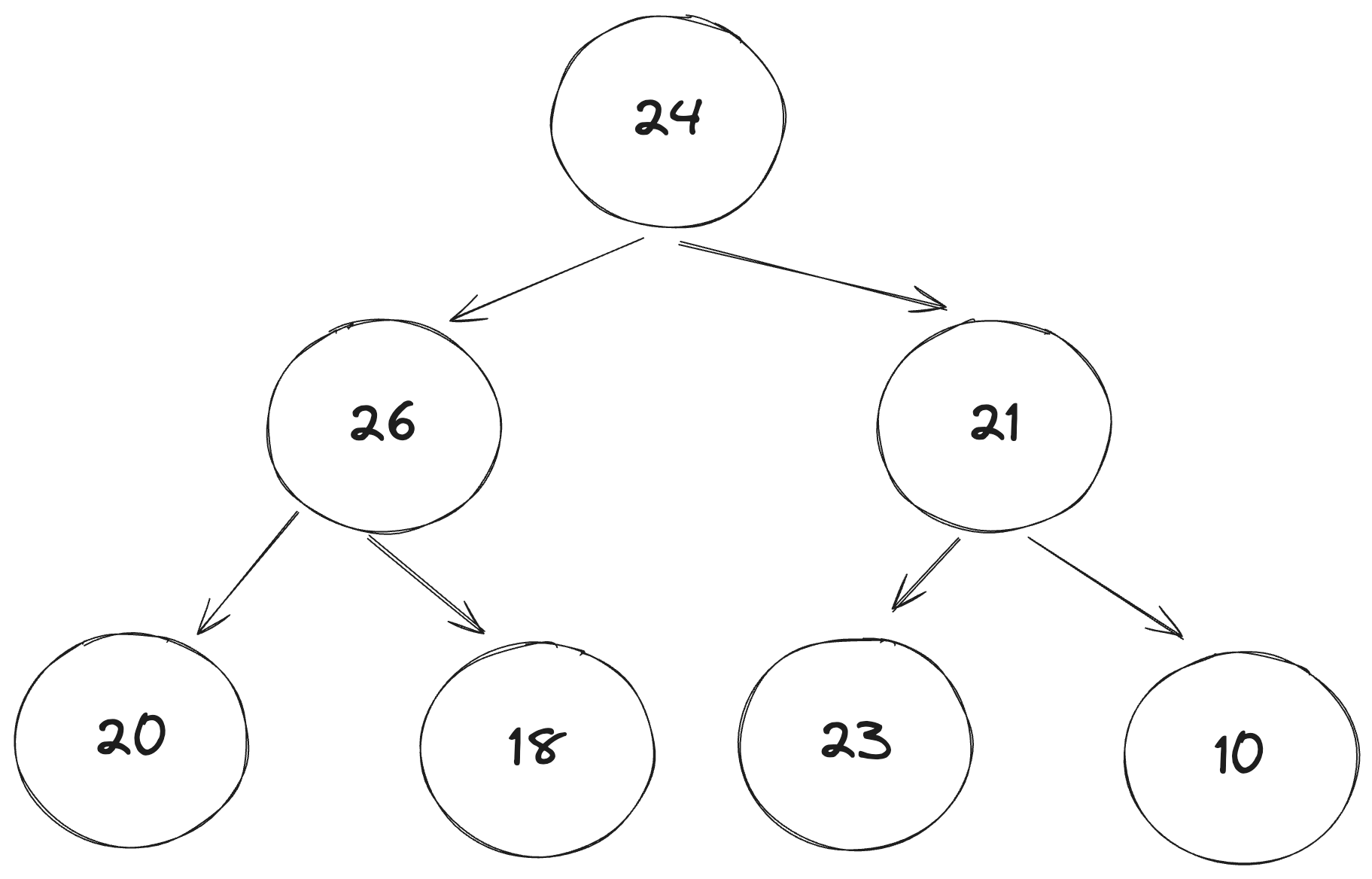
相关概念
树的相关概念会比较多,用表格梳理如下。
| 概念 | 描述 |
|---|---|
| 节点的度 | 一个节点含有的子树的个数称为该节点的度; |
| 树的度 | 一棵树中,最大的节点度称为树的度; |
| 叶节点或终端节点 | 度为零的节点 |
| 分支节点 | 度不为零的节点 |
| 父节点 | 若一个节点含有子节点,则这个节点称为其子节点的父节点; |
| 子节点 | 一个节点含有的子树的根节点称为该节点的子节点; |
| 兄弟节点 | 具有相同父节点的节点互称为兄弟节 |
| 节点的层次 | 从根开始定义起,根为第 1 层,根的子节点为第 2 层,以此类推; |
| 深度 | 对于任意节点 n,n 的深度为从根到 n 的唯一路径长,根的深度为 0; |
| 高度 | 对于任意节点 n,n 的高度为从 n 到一片树叶的最长路径长,所有树叶的高度为 0; |
树的种类
树有很多中不同的形式,下方按照不同的维度来进行划分。
有序/无序
- 无序树:树中任意节点的子节点之间没有顺序关系,这种树称为无序树,也称为自由树。
- 有序树/搜索树/查找树:树中任意节点的子节点之间有顺序关系,这种树称为有序树。即树的所有节点按照一定的顺序排列,这样进行插入、删除、查找时效率就会非常高
平衡/
节点的分叉情况
- 等叉树:是每个节点的键值个数都相同、子节点个数也都相同
- 不等叉树:每个节点的键值个数不一定相同、子节点个数也不一定相同
- B 树:对不等叉树的节点键值数和插入、删除逻辑添加一些特殊的要求,使其能达到绝对平衡的效果。B 树全称 Balance Tree。如果某个 B 树上所有节点的分叉数最大值是 m,则把这个 B 数叫做 m 阶 B 树。