堆
在计算机科学中, 一个 堆(heap) 是一种特殊的基于树的数据结构,它满足下面描述的堆属性。
- 堆中每个节点的值都大于等于(或者小于等于)其左右子节点的值。
- 堆通常是一颗
完全二叉树。
二叉堆
二叉堆是一颗完全二叉树,二叉堆分为大顶堆(最大堆)和小顶堆(最小堆)。
- 最大堆:对于每个节点的值都大于等于子树中每个节点值的堆,我们叫作 大顶堆。
- 最小堆:对于每个节点的值都小于等于子树中每个节点值的堆,我们叫作 小顶堆。
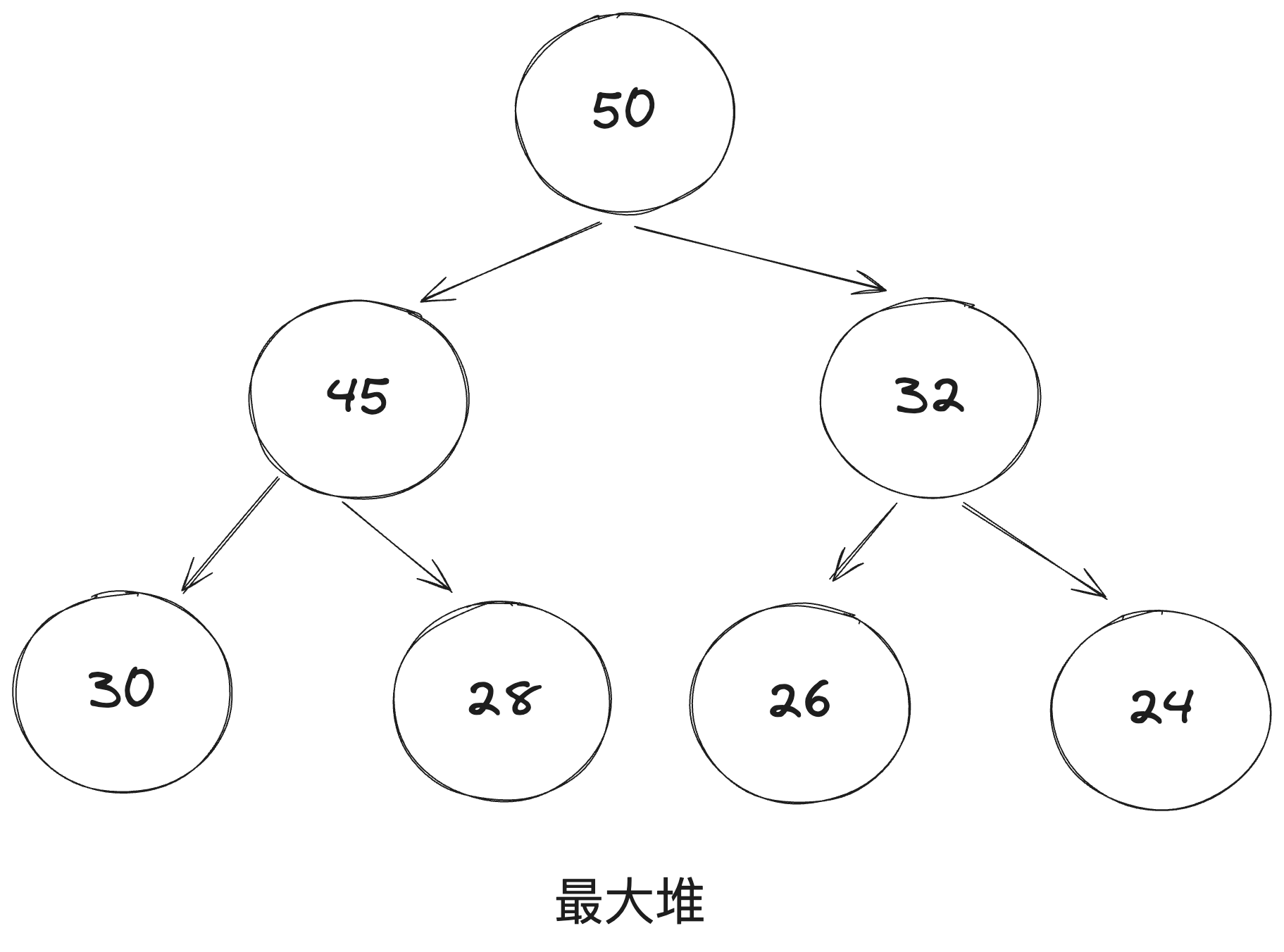
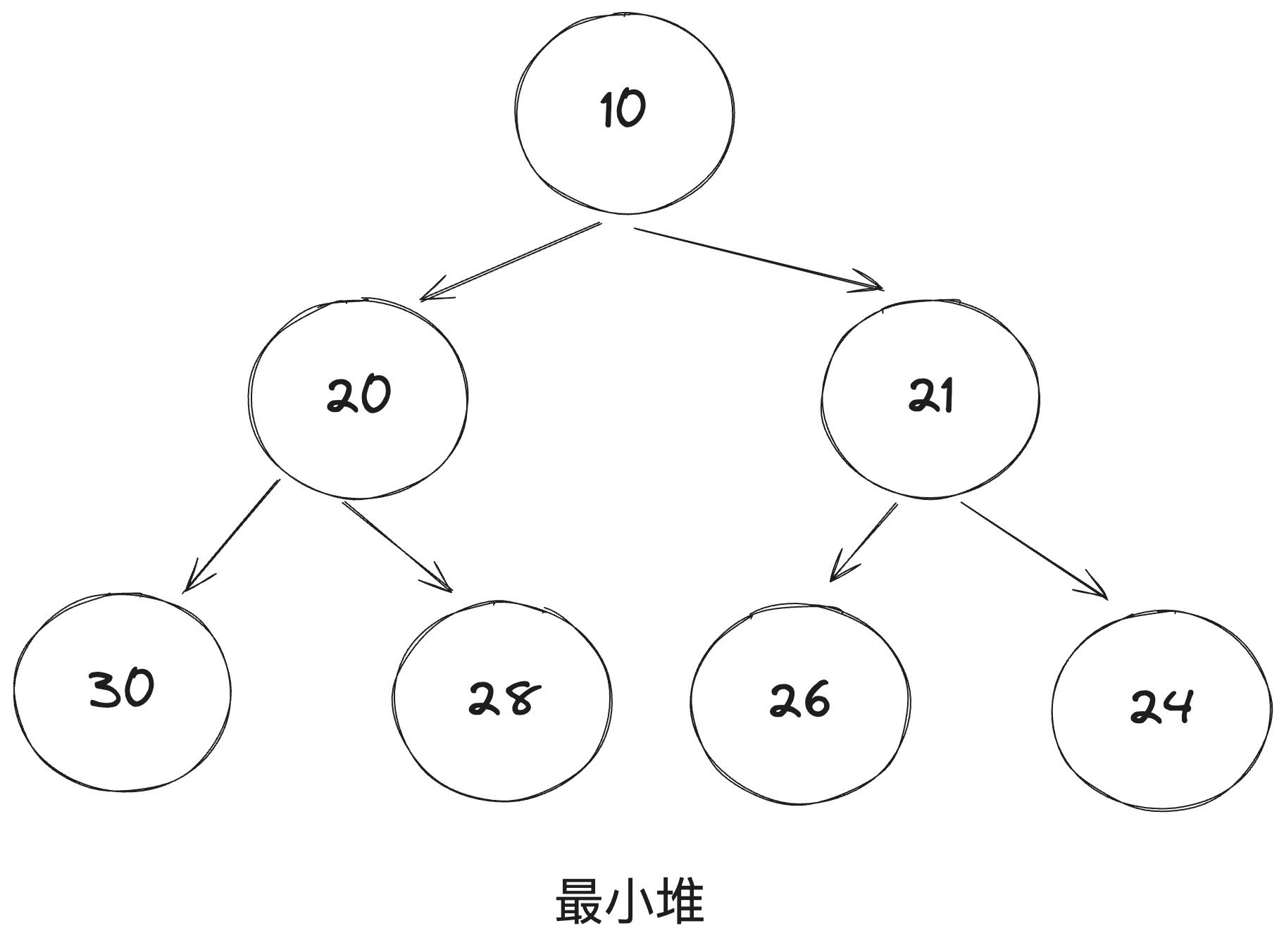
性质:
- 任何一个非树根节点的父节点为
Math.floor((index - 1) / 2) - 任何一个非叶子节点的左子节点为
index * 2 + 1 - 任何一个非叶子节点的右子节点为
index * 2 + 2
堆的操作
插入(Insert):插入是向堆中添加新元素的过程。新元素首先被添加到树的末端,然后向上移动到正确的位置以维持堆的性质。
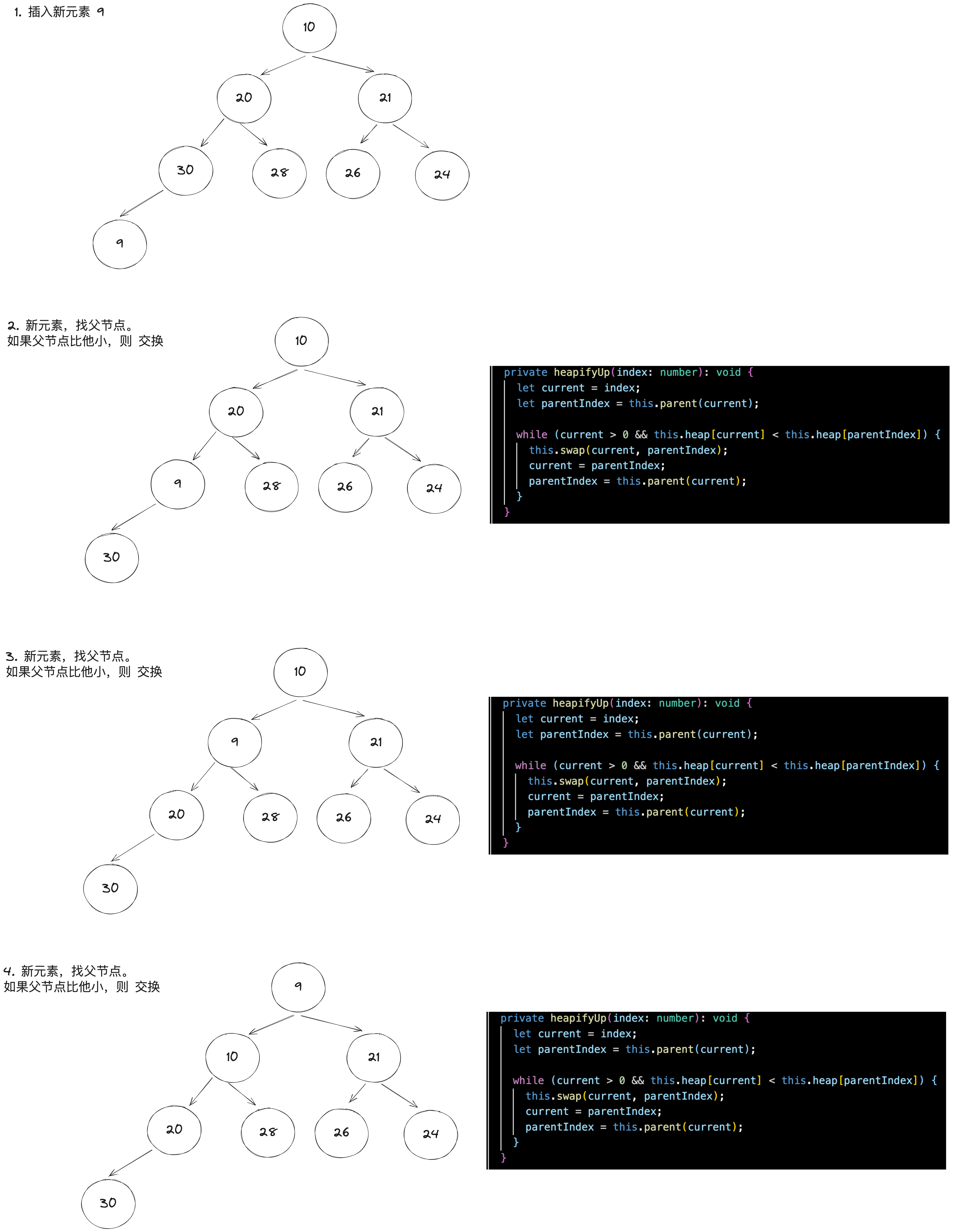
删除(Delete):在最大堆中,删除操作通常指删除最大元素,即根节点。删除根后,通常将最后一个元素移动到根位置,然后进行下沉调整。
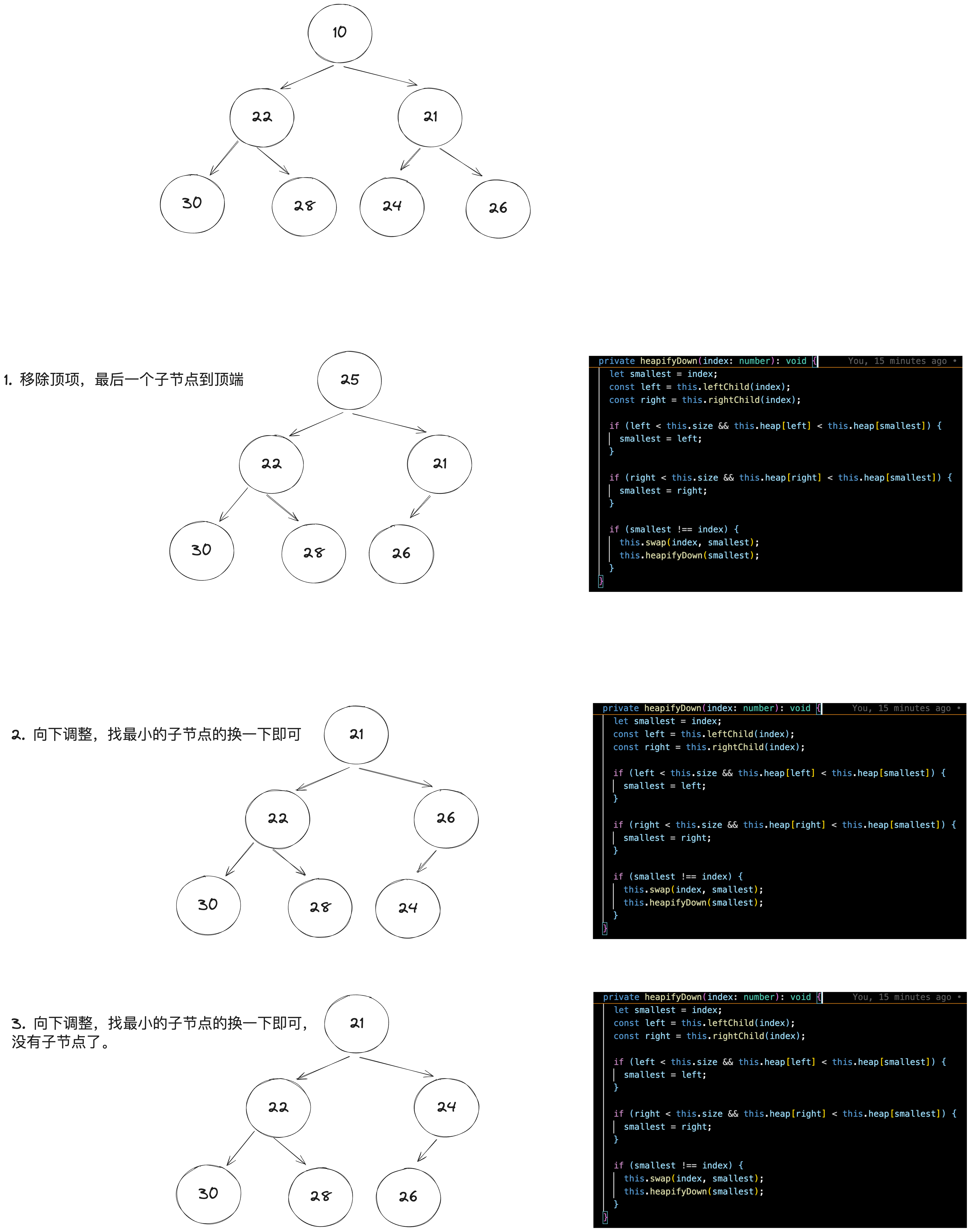
构建堆(Build Heap):给定一组元素,构建堆是将这些元素重新排列,以形成堆的过程。这可以通过从最后一个非叶子节点开始,向根节点进行下沉调整来完成。
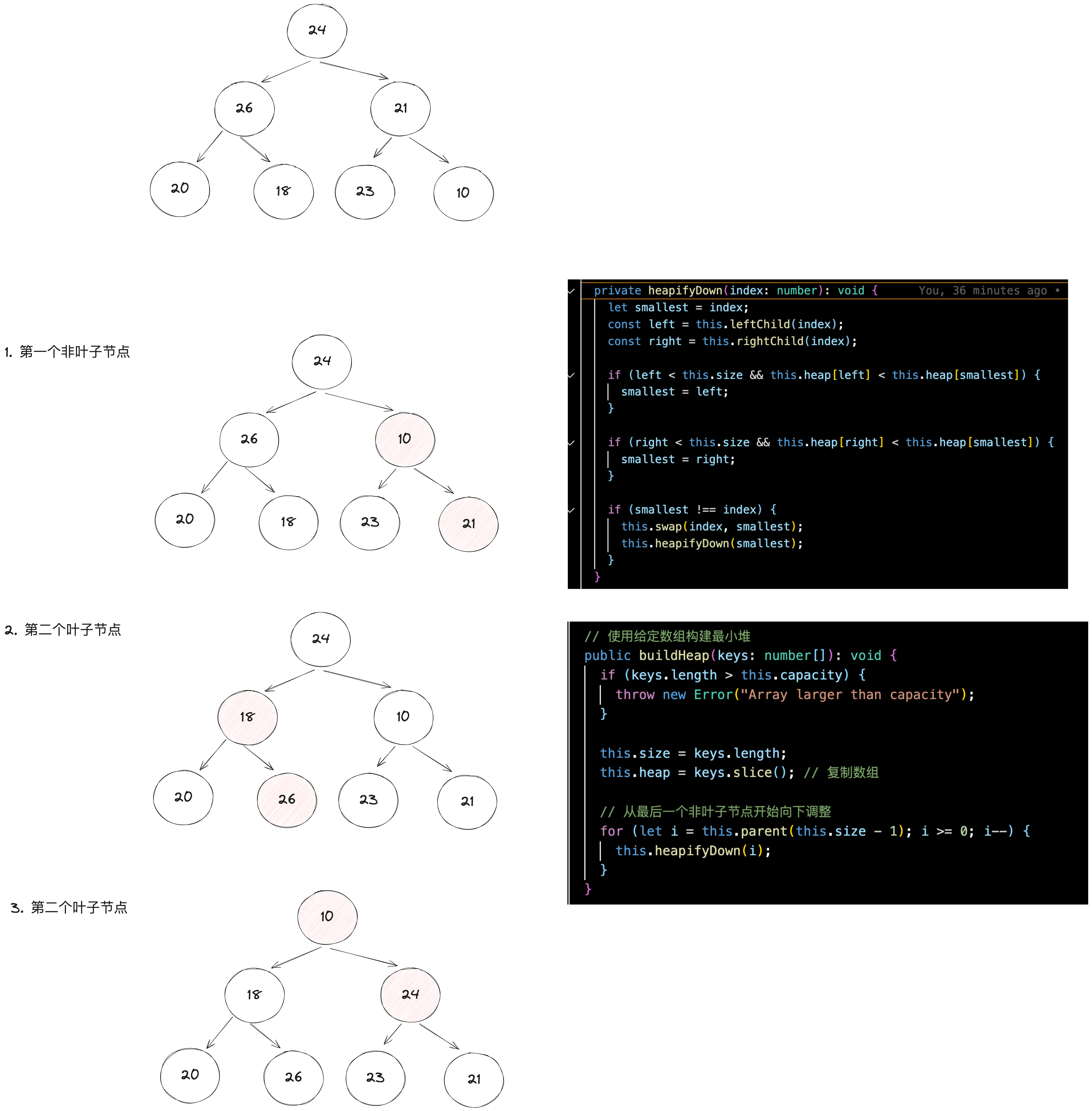
堆排序(Heap Sort):堆排序是一种利用堆结构进行排序的方法。通过构建最大堆(或最小堆),然后反复移除根节点(最大或最小值)并重新调整堆,直到堆为空,从而完成排序。
代码实现
typescript
class MinHeap {
private heap: number[];
private capacity: number;
private size: number;
constructor(capacity: number) {
this.capacity = capacity;
this.size = 0;
this.heap = new Array(capacity).fill(0);
}
private parent(i: number): number {
return Math.floor((i - 1) / 2);
}
// 获取左子节点的索引
private leftChild(i: number): number {
return 2 * i + 1;
}
// 获取右子节点的索引
private rightChild(i: number): number {
return 2 * i + 2;
}
// 交换堆中的两个元素
private swap(i: number, j: number): void {
[this.heap[i], this.heap[j]] = [this.heap[j], this.heap[i]];
}
private heapifyDown(index: number): void {
let smallest = index;
const left = this.leftChild(index);
const right = this.rightChild(index);
if (left < this.size && this.heap[left] < this.heap[smallest]) {
smallest = left;
}
if (right < this.size && this.heap[right] < this.heap[smallest]) {
smallest = right;
}
if (smallest !== index) {
this.swap(index, smallest);
this.heapifyDown(smallest);
}
}
private heapifyUp(index: number): void {
let current = index;
let parentIndex = this.parent(current);
while (current > 0 && this.heap[current] < this.heap[parentIndex]) {
this.swap(current, parentIndex);
current = parentIndex;
parentIndex = this.parent(current);
}
}
public insert(key: number): void {
if (this.size === this.capacity) {
throw new Error("Heap is full");
}
this.heap[this.size] = key;
this.size++;
this.heapifyUp(this.size - 1);
}
public extractMin(): number {
if (this.size === 0) {
throw new Error("Heap is empty");
}
const root = this.heap[0];
this.heap[0] = this.heap[this.size - 1];
this.size--;
this.heapifyDown(0);
return root;
}
// 使用给定数组构建最小堆
public buildHeap(keys: number[]): void {
if (keys.length > this.capacity) {
throw new Error("Array larger than capacity");
}
this.size = keys.length;
this.heap = keys.slice(); // 复制数组
// 从最后一个非叶子节点开始向下调整
for (let i = this.parent(this.size - 1); i >= 0; i--) {
this.heapifyDown(i);
}
}
// 使用堆排序算法对元素进行排序
public heapSort(): number[] {
const result: number[] = [];
const originalSize = this.size;
while (this.size > 0) {
result.push(this.extractMin()); // 依次取出并删除最小元素
}
this.size = originalSize; // 恢复堆的原始大小
return result;
}
}
const minHeap = new MinHeap(10);
minHeap.insert(3);
minHeap.insert(2);
minHeap.insert(15);
minHeap.insert(5);
minHeap.insert(4);
minHeap.insert(45);
console.log("Extracted Min:", minHeap.extractMin());
console.log("Heap after extracting min:", minHeap.heapSort());