完全背包问题

思路

在本节中，我们先求解另一个常见的背包问题：完全背包，再了解它的一种特例：零钱兑换。

给定 𝑛 个物品，第 𝑖 个物品的重量为 𝑤𝑔𝑡[𝑖−1]、价值为 𝑣𝑎𝑙[𝑖−1] ，和一个容量为 𝑐𝑎𝑝 的背包。**每个物品可以重复选取**，问在限定背包容量下能放入物品的最大价值。示例如图 14-22 所示。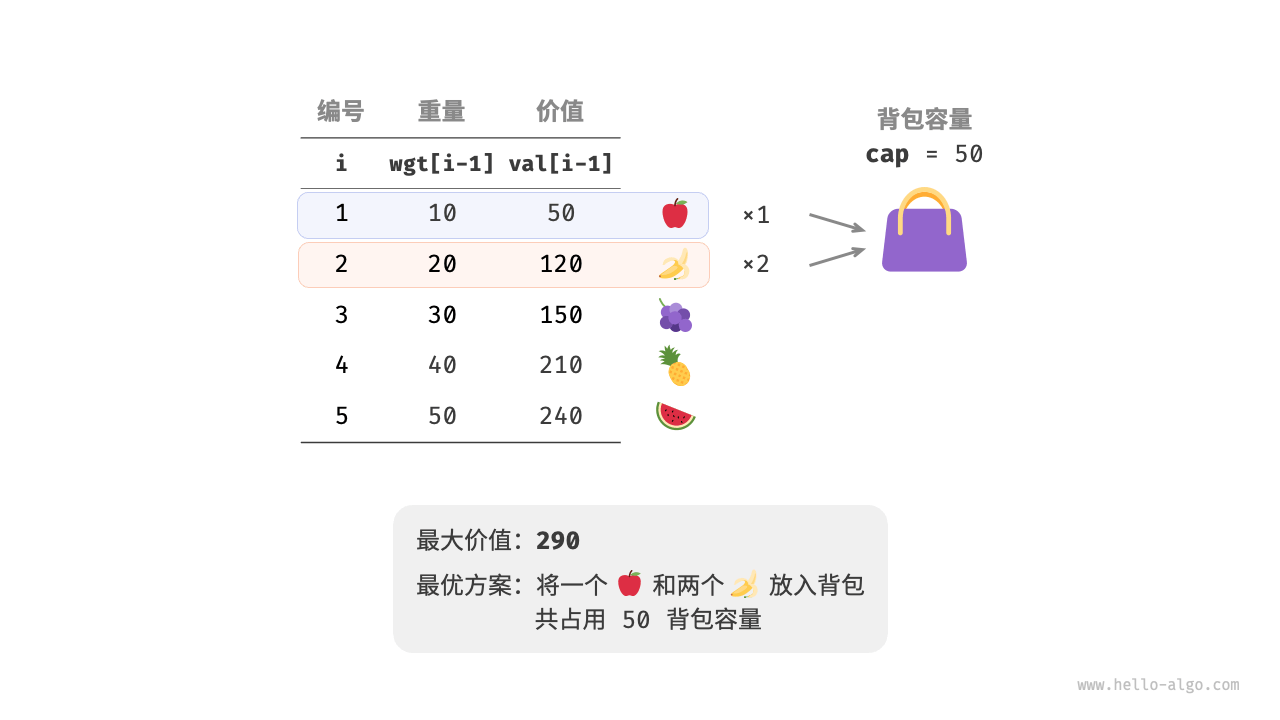

完全背包问题和 0-1 背包问题非常相似，区别仅在于不限制物品的选择次数。

在 0-1 背包问题中，每种物品只有一个，因此将物品 𝑖 放入背包后，只能从前 𝑖−1 个物品中选择。
在完全背包问题中，每种物品的数量是无限的，因此将物品 𝑖 放入背包后，仍可以从前 𝑖 个物品中选择。

在完全背包问题的规定下，状态 [𝑖,𝑐] 的变化分为两种情况。

不放入物品 𝑖 ：与 0-1 背包问题相同，转移至 [𝑖−1,𝑐] 。
放入物品 𝑖 ：与 0-1 背包问题不同，转移至 [𝑖,𝑐−𝑤𝑔𝑡[𝑖−1]] 。所以状态转移方程变成了

dp[i, c] = max(dp[i-1, c], dp[i, c - wgt[i - 1]] + val[i - 1])

代码实现

function unboundedKnapsackDP(
  wgt: Array<number>,
  val: Array<number>,
  cap: number
) {
  const n = wgt.length;

  const dp = Array.from({ length: n + 1 }, () => Array.from({ length: cap + 1 }, () => 0));

  for (let i = 1; i <= n; i++) {
    for (let c = 1; c <= cap; c++) {
      if (wgt[i-1] > c) {
        dp[i][c] = dp[i -1][c]; 
      } else {
        dp[i][c] = Math.max(
          dp[i - 1][c],
          dp[i][c - wgt[i-1]] + val[i-1]
        )
      }
    }
  }

  return dp[n][cap];
}

零钱兑换问题

给定 𝑛 种硬币，第 𝑖 种硬币的面值为 𝑐𝑜𝑖𝑛𝑠[𝑖−1] ，目标金额为 𝑎𝑚𝑡 ，**每种硬币可以重复选取**，问能够凑出目标金额的最少硬币数量。如果无法凑出目标金额，则返回 −1 。示例如图 14-24 所示。

思路

零钱兑换可以看作完全背包问题的一种特殊情况，两者具有以下联系与不同点。

两道题可以相互转换，“物品”对应“硬币”、“物品重量”对应“硬币面值”、“背包容量”对应“目标金额”。
优化目标相反，完全背包问题是要最大化物品价值，零钱兑换问题是要最小化硬币数量。
完全背包问题是求“不超过”背包容量下的解，零钱兑换是求“恰好”凑到目标金额的解。

第一步：思考每轮的决策，定义状态，从而得到 𝑑𝑝 表

状态 [𝑖,𝑎] 对应的子问题为：前 𝑖 种硬币能够凑出金额 𝑎 的最少硬币数量，记为 𝑑𝑝[𝑖,𝑎] 。

二维 𝑑𝑝 表的尺寸为 (𝑛+1)×(𝑎𝑚𝑡+1) 。

第二步：找出最优子结构，进而推导出状态转移方程

本题与完全背包问题的状态转移方程存在以下两点差异。

本题要求最小值，因此需将运算符 max() 更改为 min() 。
优化主体是硬币数量而非商品价值，因此在选中硬币时执行 +1 即可。

𝑑𝑝[𝑖,𝑎]=min(𝑑𝑝[𝑖−1,𝑎],𝑑𝑝[𝑖,𝑎−𝑐𝑜𝑖𝑛𝑠[𝑖−1]]+1)

第三步：确定边界条件和状态转移顺序

当目标金额为 0 时，凑出它的最少硬币数量为 0 ，即首列所有 𝑑𝑝[𝑖,0] 都等于 0 。

当无硬币时，无法凑出任意 >0 的目标金额，即是无效解。为使状态转移方程中的 min() 函数能够识别并过滤无效解，我们考虑使用 +∞ 来表示它们，即令首行所有 𝑑𝑝[0,𝑎] 都等于 +∞ 。

代码实现

function coinChangeDP(coins: Array<number>, amt: number): number {
  const n = coins.length;
  const MAX = amt + 1;

  const dp = Array.from({ length: n + 1 }, () => 
    Array.from({ length: amt + 1 }, () => 0)
  );
  
  for (let a = 1; a <= amt; a++) {
    dp[0][a] = MAX;
  } 
  
  for (let i = 1; i <= n; i++) {
    for (let a = 1; a <= amt; a++) {
      if (coins[i-1] > a) {
        dp[i][a] = dp[i - 1][a];
      } else {
        dp[i][a] = Math.min(dp[i-1][a], dp[i][a - coins[i - 1]] + 1);  
      }
    }
  }

  return dp[n][amt] !== MAX ? dp[n][amt] : -1;
}

参考

https://www.hello-algo.com/chapter_dynamic_programming/unbounded_knapsack_problem/#3_2

完全背包问题 ​